Stochastik – Beispielaufgaben und Lösungswege

Um Wahrscheinlichkeiten für Ereignisse zu bestimmen, muß man häufig Verteilungen benutzen. Anhand von drei Beispielen möchten wir Ihnen die Verwendung der zumeist verwendeten deutlich machen: Die Binomial-, die hypergeometrische und die Normalverteilung.

Beispielaufgabe S1 zeigt

• die Binomialverteilung

Beispielaufgabe S2 zeigt

• die hypergeometrische Verteilung

Beispielaufgabe S3 zeigt

• die Normalverteilung

S1. Aufgabe

Wie groß ist die Wahrscheinlichkeit bei 10 Würfen mit einem idealen Würfel höchstens 3 Mal die Augenzahl 1 zu erhalten?

Arbeitsschritte zur Lösung:

Starten Sie Stochastik. Die gesuchte Verteilung ist offensichtlich die Binomialverteilung, denn als Urnenmodell ist das folgende passend.

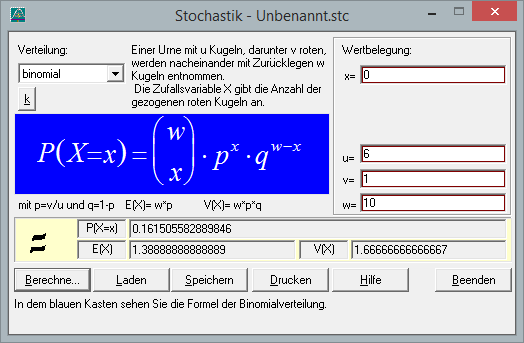
Urnenmodell: Aus einer Urne mit 6 Kugeln (die verschiedenen Augenzahlen des Würfels), darunter 1 rote (die Augenzahl 1), werden nacheinander mit Zurücklegen n=0,1,2,3 Kugeln entnommen (es soll höchstens 3 Mal eine 1 geworfen werden, d.h. es kann auch kein Mal eine 1 geworfen werden).

Gesucht ist also

Wählen Sie also aus und berechnen Sie P(X=0). Setzen Sie dafür die Variablen x=0, u=6, v=1 und w=10 ein und drücken Sie . Sie erhalten dann für

P(X=0)0.161505582889846

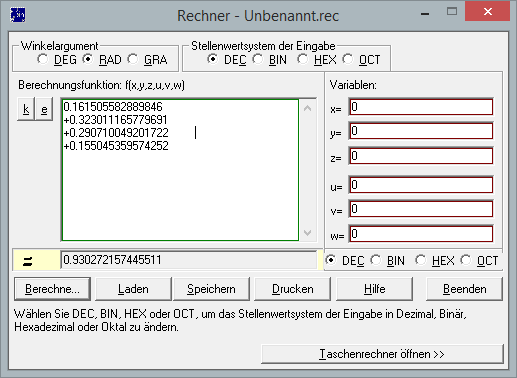
Verfahren Sie analog weiter mit P(X=1) , P(X=2) , P(X=3) und Sie erhalten

P(X=1)0.323011165779691

P(X=2)0.290710049201722

P(X=3)0.155045359574252

Addieren Sie diese Werte mit dem  Rechner, so erhalten Sie als Wert 0.930272157445511 und Sie können die Frage beantworten.

Die Wahrscheinlichkeit bei 10 Würfen mit einem idealen Würfel höchstens 3 Mal die Augenzahl 1 zu erhalten ist 93 Prozent.

In diesem Zusammenhang ist der Erwartungswert E(X)=1.3 interessant. Dieser besagt, dass man erwarten kann, bei 10 Würfen mit einem idealen Würfel wenigsten 1 Mal als Augenzahl eine 1 zu erhalten (eigentlich 1.3 Mal, ist aber nicht besonders anschaulich).

S2. Aufgabe

Wie groß ist die Wahrscheinlichkeit, dass Sie im Lotto (ohne Zusatzzahl) 6 Richtige haben?

Arbeitsschritte zur Lösung:

Starten Sie Stochastik. Die gesuchte Verteilung ist offensichtlich die hypergeometrische, denn als Urnenmodell ist das folgende passend.

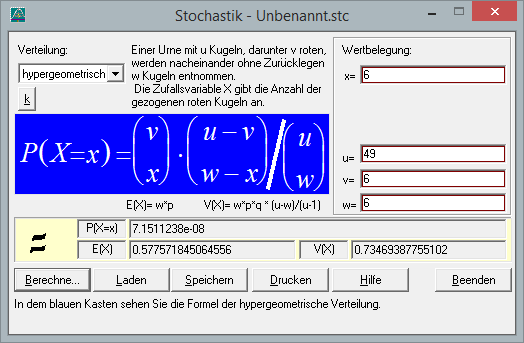
Urnenmodell: Aus einer Urne mit 49 Kugeln (die numerierten Lottokugeln), darunter 6 rote (Ihre getippten Zahlen), werden nacheinander mit Zurücklegen 6 Kugeln entnommen.

Wählen Sie also aus und berechnen Sie P(X=6). Setzen Sie dafür die Variablen x=6, u=49, v=6 und w=6 ein und drücken Sie . Sie erhalten dann für

P(X=6)7.1511238e-08 (=0.000000071511238)

und können die Frage beantworten.

Die Wahrscheinlichkeit, dass Sie im Lotto (ohne Zusatzzahl) 6 Richtige haben ist 0.00000715 Prozent (d.h., wenn Sie 14 Millionen verschiedene Tippreihen für ein Spiel ausgefüllt haben, sollte eine richtige darunter sein).

S3. Aufgabe

Sei die Zufallsvariable X normalverteilt mit dem Erwartungswert m=1.2 und der Varianz s²=. Berechnen Sie: P(X ).

Arbeitsschritte zur Lösung:

Starten Sie Stochastik. Wählen Sie die Normalverteilung über aus und berechnen Sie P(X ). Setzen Sie dafür die Variablen x=sqrt(2), y=1.2 und z=1/sqrt(2) ein und drücken Sie . Sie erhalten dann für

P(X)0.619031.

Möchten Sie sich aus Interesse die Gaußsche Glockenkurve dieser Normalverteilung ansehen, so wählen Sie zum Kopieren der Verteilung und starten Sie Funktionsdiskussion. Drücken Sie dann das Schaltfeld und danach  zum Einfügen der Verteilungsfunktion. Nachdem Sie gedrückt haben, sehen Sie in dem Zeichnungsfenster die Funktion (der Mittelpunkt der Glockenkurve ist bei 1.2 also bei dem Erwartungswert m).