Matrixdiskussion – Beispielaufgaben und Lösungswege

Mit diesem Teilprogramm können Sie quadratische Matrizen auf ihre Eigenschaften hin untersuchen. Da eine inverse Matrix nur zu einer quadratischen Matrix existiert, wurde der Einfachheit halber auf eine Eingabe nicht-quadratischer Matrizen verzichtet. Gleiches gilt für Eigenwerte, die auch nur über quadratische Matrizen bestimmt werden können.

Möchten Sie zu einer nicht-quadratischen Matrix den Rang bestimmen, so müssen Sie nur die übrigen Elemente mit 0 vorgeben.

Beispielaufgabe MD1 zeigt

1. die Bestimmung der inversen Matrix.
2. die Bestimmung der Determinante.
3. die Bestimmung des charakteristischen Polynoms und der Eigenwerte.

Zudem finden Sie am Ende der Seite allgemeine Anmerkungen und Tipps zur Matrixdiskussion.

MD1. Aufgabe

Gegeben sei die reelle quadratische Matrix

1. Ermitteln Sie, ob die Matrix A eine Inverse A-1 besitzt und bestimmen Sie diese, falls eine existiert.
2. Im weiteren bestimmen Sie die Determinante Det(A)=|A|.
3. Bestimmen Sie dann das charakteristische Polynom der Matrix A und die Eigenwerte von A.

Arbeitsschritte zur Lösung:

Starten Sie Matrixdiskussion und geben Sie als Ordnung eine 3 ein. Drücken Sie dann die Schaltfläche , um die Eingabe zu übernehmen. In den folgenden Dialog geben Sie die Matrix A ein und drücken hier auch auf .

Nun sehen Sie schon alle Informationen, um zu entscheiden, ob die Matrix A eine Inverse A-1 besitzt. Da der Rang der Matrix gleich 3 ist, folgt, dass eine Inverse existieren muss. (Dies folgt auch aus Det(A)0.) Sie sehen zunächst die Ausgangsmatrix angegeben. Um die inverse Matrix zu erhalten, drücken Sie auf die Schaltfläche . Nachfolgend können Sie also schon die 1. Frage beantworten.

1. die Inverse Matrix

Es existiert eine Inverse A-1 und zwar

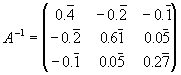
Die Antwort zur 2. Frage lesen Sie einfach ab.

2. die Determinante der Matrix

Die Determinate Det(A)=18.

3. das charakteristische Polynom und die Eigenwerte der Matrix

Zur Bestimmung der Eigenwerte drücken Sie die Schaltfläche . Zuerst wird nun das charakteristische Polynom bestimmt. Dies kann u.U. längere Zeit in Anspruch nehmen. Danach wird der eigentliche Dialog zur Bestimmung der Eigenwerte angezeigt. Es werden drei unabhängig voneinander arbeitende Verfahren zur Berechnung verwendet, wobei das zweite und dritte nur ausgeführt werden, wenn Eigenwerte ungleich 0 existieren.

Starten Sie die Eigenwertbestimmung mit der Schaltfläche . Über das erste und zweite Verfahren werden nun die Eigenwerte bestimmt. Für das dritte Verfahren wird dann der benötigte Abstand zwischen zwei Eigenwerten abgefragt. I.A. ist der vorgegebene Wert ausreichend und Sie übernehmen dann mit die Eingabe. Drücken Sie wenn auch das dritte Verfahren abgeschlossen ist. Nun könne Sie die Antwort zur 3. Frage ablesen.

Das charakteristische Polynom p(x) der Matrix A ist

und alle drei Verfahren liefern als Eigenwerte x11.267949192, x2=3 und x34.732050808.

Möchten Sie sich aus Interesse die zugehörige Funktion ansehen, so wählen Sie  zum Kopieren des charakteristischen Polynoms und starten Sie Funktionsdiskussion. Drücken Sie dann das Schaltfeld  und danach  zum Einfügen der Funktion. Nachdem Sie  gedrückt haben, sehen Sie in dem Zeichnungsfenster die Funktion des charakteristischen Polynoms.

Allgemeine Anmerkungen und Tipps zur Matrixdiskussion

Es ist zu beachten, dass u.U. die drei Verfahren für die Bestimmung der Eigenwerte unterschiedliche Werte liefern können. Dies kann passieren, wenn die Elemente der Matrix zu groß sind und dadurch das charakteristische Polynom insgesamt nicht genau bestimmt werden kann.