 Funktionsdiskussion – Beispielaufgaben und Lösungswege
Funktionsdiskussion – Beispielaufgaben und Lösungswege
Die Funktionsdiskussion ist die wohl interessanteste Anwendung. Hier kann man sich eine zwei- oder dreidimensionale Funktion ansehen und die Funktionsauswertung einer zweidimensionalen Funktion durchführen.
Beispielaufgabe FD1 zeigt
- die Bestimmung von Nullstellen, Extrema und Wendepunkte.
- die Bestimmung des Integrals über einem Intervall.
- die Bestimmung der 1. Ableitung.
Beispielaufgabe FD2 zeigt
- die Lösung einer Gleichung
Beispielaufgabe FD3 zeigt
- die Lösung einer Ungleichung
Beispielaufgabe FD4 zeigt
- die Lösung eines Limes
Beispielaufgabe FD5 zeigt
- die Untersuchung einer dreidimensionalen Funktion
Zudem finden Sie am Ende der Seite allgemeine Anmerkungen und Tipps zur Funktionsdiskussion.
Arbeitsschritte zur Lösung:
Starten Sie ![]() Funktionsdiskussion und drücken Sie dann das Schaltfeld
Funktionsdiskussion und drücken Sie dann das Schaltfeld ![]() . Geben Sie die obige Funktion ein:
. Geben Sie die obige Funktion ein:
f(x)= sqrt( -x*(x-3)*(x^2-(10/3)*x+4) )
Markieren Sie dann die Felder ![]() ,
, ![]() und
und ![]() . Wählen Sie als Bereich das Intervall [x1,x2]=[-2,5] und [h1,h2]=[-2,5], indem Sie diesen Bereich in die entsprechenden Felder eingeben oder die Felder
. Wählen Sie als Bereich das Intervall [x1,x2]=[-2,5] und [h1,h2]=[-2,5], indem Sie diesen Bereich in die entsprechenden Felder eingeben oder die Felder ![]()
![]() ,
, ![]() und
und ![]()
![]() zur Bildsteuerung verwenden, bis der Bereich überlappt wird. Drücken Sie dann
zur Bildsteuerung verwenden, bis der Bereich überlappt wird. Drücken Sie dann ![]() , so dass die Skalierung sowie der Abstand für die Funktionsdiskussion und die Genauigkeit der Integralberechnung zur Funktion passend bestimmt werden.
, so dass die Skalierung sowie der Abstand für die Funktionsdiskussion und die Genauigkeit der Integralberechnung zur Funktion passend bestimmt werden.
Sie erhalten auch eine ungefähre Zeit für die auszuführenden Berechnungen. Bestätigen Sie dann mit ![]() die Eingaben und drücken Sie im darauf folgenden Berechnungsdialog die Schaltfläche
die Eingaben und drücken Sie im darauf folgenden Berechnungsdialog die Schaltfläche ![]() . Nach dem Ende der Berechnungen drücken Sie
. Nach dem Ende der Berechnungen drücken Sie ![]() und lesen Sie einfach die ermittelten Werte ab.
und lesen Sie einfach die ermittelten Werte ab.
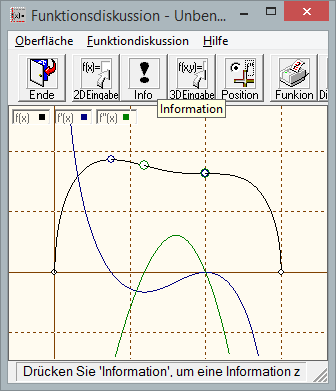
1. die Nullstellen, Extrema und Wendepunkte:
Die Nullstellen sind x1=0 und x2=3.
Ein Hochpunkt ist bei xhp=0.75 und ein Sattelpunkt bei xsp=2.
Die Wendestellen sind bei xrl![]() 1.188599882 (rechts/ links Wendestelle) und xlr=2 (links/ rechts Wendestelle).
1.188599882 (rechts/ links Wendestelle) und xlr=2 (links/ rechts Wendestelle).
2. das Integral über dem Intervall [x1,x2]=[-2,5]:
Das im Beispielfall bei einer Genauigkeit von ungefähr 1981.118 ermittelte Integral ist I![]() 4.697493625.
4.697493625.
3. die 1. Ableitung:
Die 1. Ableitung ist
f'(x)= -(((((x-3)+x)*((x^2-((10/3)*x))+4))+(((x-3)*x)*((2*x)-(10/3))))/(2*sqrt(-(((x^2-((10/3)*x))+4)*((x-3)*x)))))
also
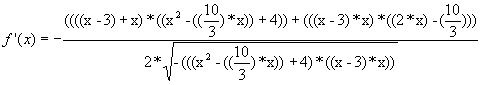
Arbeitsschritte zur Lösung:
Starten Sie ![]() Funktionsdiskussion und drücken Sie dann das Schaltfeld
Funktionsdiskussion und drücken Sie dann das Schaltfeld ![]() . Die obige Gleichung entspricht
. Die obige Gleichung entspricht
Demnach werden die Nullstellen von der Funktion
gesucht. Also geben Sie zur Lösung die Funktion f(x) ein:
f(x)= exp(x^2+x)/exp(2) -1
Markieren Sie dann die Felder ![]() und
und ![]() . Wählen Sie als Bereich das Intervall groß genug, z.B. [x1,x2]=[-100,100] und [h1,h2]=[-100,100]. Drücken Sie dann
. Wählen Sie als Bereich das Intervall groß genug, z.B. [x1,x2]=[-100,100] und [h1,h2]=[-100,100]. Drücken Sie dann ![]() , so dass die Skalierung sowie der Abstand für die Funktionsdiskussion passend bestimmt werden. Bestätigen Sie dann mit
, so dass die Skalierung sowie der Abstand für die Funktionsdiskussion passend bestimmt werden. Bestätigen Sie dann mit ![]() die Eingaben und drücken Sie im darauf folgenden Berechnungsdialog die Schaltfläche
die Eingaben und drücken Sie im darauf folgenden Berechnungsdialog die Schaltfläche ![]() . Nach dem Ende der Berechnungen drücken Sie
. Nach dem Ende der Berechnungen drücken Sie ![]() und lesen Sie einfach die ermittelten Werte ab.
und lesen Sie einfach die ermittelten Werte ab.
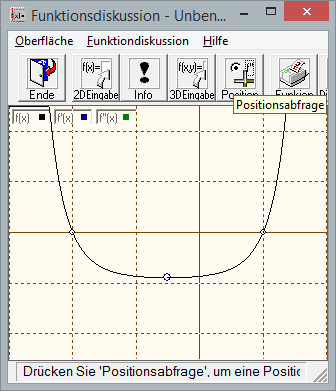
Die Lösung der Gleichung
Die Nullstellen sind x1=-2 und x2=1 und dies sind auch die Lösungen der Gleichung.
Arbeitsschritte zur Lösung:
Starten Sie ![]() Funktionsdiskussion und drücken Sie dann das Schaltfeld
Funktionsdiskussion und drücken Sie dann das Schaltfeld ![]() . Die obige Ungleichung entspricht
. Die obige Ungleichung entspricht
Demnach werden die Stellen gesucht mit
gesucht. Also geben Sie zur Lösung die Funktion f(x) ein:
f(x)= (x^2-11*x)/(x+16) -abs(x-1)
Markieren Sie dann die Felder ![]() und
und ![]() . Wählen Sie als Bereich das Intervall groß genug, z.B. [x1,x2]=[-100,100] und [h1,h2]=[-100,100]. Drücken Sie dann
. Wählen Sie als Bereich das Intervall groß genug, z.B. [x1,x2]=[-100,100] und [h1,h2]=[-100,100]. Drücken Sie dann ![]() , so dass die Skalierung sowie der Abstand für die Funktionsdiskussion passend bestimmt werden.
, so dass die Skalierung sowie der Abstand für die Funktionsdiskussion passend bestimmt werden.
Wenn Sie ![]() wählen, wird Ihnen auffallen, dass eine mögliche Nullstelle im Bereich -16 erst jetzt angezeigt wird. In der Umgebung dieses Punktes ist die Steigung so stark, dass der h-Sprung nicht angezeigt werden konnte. Dies bedeutet, dass eventuell die Funktionsdiskussion nicht genau entscheiden kann, ob in dem Punkt tatsächlich eine Nullstelle ist. Wählen Sie aus diesem Grund
wählen, wird Ihnen auffallen, dass eine mögliche Nullstelle im Bereich -16 erst jetzt angezeigt wird. In der Umgebung dieses Punktes ist die Steigung so stark, dass der h-Sprung nicht angezeigt werden konnte. Dies bedeutet, dass eventuell die Funktionsdiskussion nicht genau entscheiden kann, ob in dem Punkt tatsächlich eine Nullstelle ist. Wählen Sie aus diesem Grund ![]() an, wodurch alle Kandidaten für Nullstellen (auch der Ableitungen) ausgegeben werden.
an, wodurch alle Kandidaten für Nullstellen (auch der Ableitungen) ausgegeben werden.
Bestätigen Sie dann mit ![]() die Eingaben und drücken Sie im darauf folgenden Berechnungsdialog die Schaltfläche
die Eingaben und drücken Sie im darauf folgenden Berechnungsdialog die Schaltfläche ![]() . Nach dem Ende der Berechnungen drücken Sie
. Nach dem Ende der Berechnungen drücken Sie ![]() und lesen Sie einfach die ermittelten Werte ab.
und lesen Sie einfach die ermittelten Werte ab.
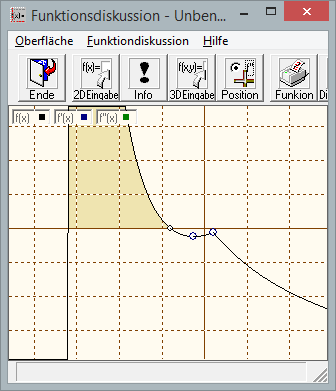
Die Lösung der Ungleichung
Die ermittelten Nullstellen sind x1=-16 und x2=-4. Da die im Punkt -16 erzwungen wurde, müssen Sie diesen noch näher untersuchen. Es ergibt sich dann, dass -16 nicht eingesetzt werden kann, da der Limes
nicht definiert ist. Sie sehen in der Zeichnung der Funktion, den Bereich über 0, was die Bedingung war.
Demnach ist die Lösung: L=]-16,-4[ (exklusive -16 und -4, da die Funktion im Punkt -16 nicht definiert und -4 gleich 0 ist).
Arbeitsschritte zur Lösung:
Starten Sie ![]() Funktionsdiskussion und drücken Sie dann das Schaltfeld
Funktionsdiskussion und drücken Sie dann das Schaltfeld ![]() . Die obige Funktion ist
. Die obige Funktion ist
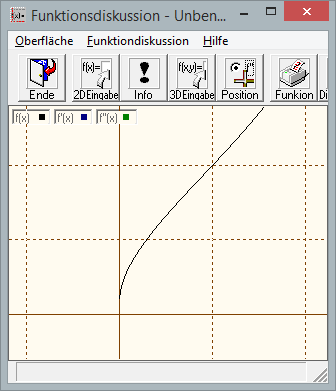
f(x)= (exp(x-1)+exp(1-x)-2) / ((x-1)-ln(x))
Sie sehen an der Zeichnung sofort, dass im Punkt 1 der Wert gleich 2 ist.
Also folgt die Behauptung, die erst noch bewiesen werden muss:
Arbeitsschritte zur Lösung:
Starten Sie ![]() Funktionsdiskussion und drücken Sie dann das Schaltfeld
Funktionsdiskussion und drücken Sie dann das Schaltfeld ![]() . Die obige Funktion ist
. Die obige Funktion ist
f(x,y)= –x^2+y^2
und verwenden Sie die Schaltflächen zur Zeichnungsänderung, um einen guten Blick auf den Nullpunkt zu haben. Auch empfiehlt es sich für die Zeichnung ![]() und
und ![]() anzuwählen. Bestätigen Sie dann mit
anzuwählen. Bestätigen Sie dann mit ![]() die Eingaben und drücken Sie im Zeichnungsfenster die Schaltfläche
die Eingaben und drücken Sie im Zeichnungsfenster die Schaltfläche ![]() zur Positionsabfrage. In dem darauf folgenden Dialog können nun Positionen näher untersucht werden. Geben Sie als x- und y- Wert jeweils eine 0 ein.
zur Positionsabfrage. In dem darauf folgenden Dialog können nun Positionen näher untersucht werden. Geben Sie als x- und y- Wert jeweils eine 0 ein.
Bestimmen Sie nun den Gradienten
![]()
im Punkt (0,0). Wählen Sie dazu ![]() für die 1. Richtungsableitung nach x im Punkt (0,0) an. Drücken Sie dann die Schaltfläche
für die 1. Richtungsableitung nach x im Punkt (0,0) an. Drücken Sie dann die Schaltfläche ![]() und Sie erhalten
und Sie erhalten
![]()
Wählen Sie nun ![]() für die 1. Richtungsableitung nach y im Punkt (0,0) an. Drücken Sie die Schaltfläche
für die 1. Richtungsableitung nach y im Punkt (0,0) an. Drücken Sie die Schaltfläche ![]() und Sie erhalten
und Sie erhalten
![]()
Also insgesamt:
Demnach könnte im Nullpunkt ein lokales Extremum liegen.
Bestimmen Sie nun die Hessesche Matrix
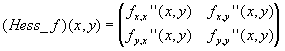
im Punkt (0,0). Wählen Sie dazu ![]() an für die 1. Richtungsableitung nach x und die 2. Richtungsableitung nach y im Punkt (0,0). Drücken Sie dann die Schaltfläche
an für die 1. Richtungsableitung nach x und die 2. Richtungsableitung nach y im Punkt (0,0). Drücken Sie dann die Schaltfläche ![]() und Sie erhalten
und Sie erhalten
![]()
Verfahren Sie analog mit den weiteren Ableitungen und Sie erhalten insgesamt:
![]()
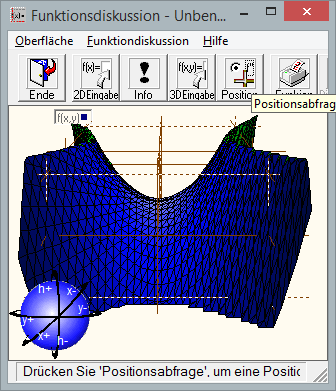
Diese Matrix ist offensichtlich indefinit denn Sie besitzt einen positiven und negativen Eigenwert, also folgt insgesamt, dass im Nullpunkt kein lokales Extremum liegt. Der Graph bildet nämlich nach der Zeichnung eine sogenannte Sattelfläche, wie im Bild zu sehen ist.
Allgemeine Anmerkungen und Tipps zur Funktionsdiskussion
Bitte beachten Sie, dass sowohl die Funktionsdiskussion als auch die Integralberechnung nur über dem gewählten [x1,x2]- Bereich durchgeführt wird. Falls kein x-Intervall in einer Funktionsdiskussionsaufgabe angegeben ist, so sollte dieses zur Bestimmung der Nullstellen, Extrema und Wendepunkte angemessen groß gewählt werden, z.B. [x1,x2]=[-100,100] und [h1,h2]=[-100,100]. Die benötigten Intervallgrenzen können Sie am einfachsten ersehen, indem Sie die Ableitungen f ’(x) und f ’’(x) zeichnen lassen.
Mit der Genauigkeit der Integralberechnung steigt die Genauigkeit des Ergebnisses. D.h. im obigen Beispiel FD1. wurde bei einer Genauigkeit von 1981.118 als Integral I![]() 4.697493625 ermittelt. Bei einer Genauigkeit von 36090.03 würde I
4.697493625 ermittelt. Bei einer Genauigkeit von 36090.03 würde I![]() 4.697497972 ermittelt werden, wobei das exakte Ergebnis bei I
4.697497972 ermittelt werden, wobei das exakte Ergebnis bei I![]() 4.697498056 liegt. Also im 1. Fall ist das Ergebnis
4.697498056 liegt. Also im 1. Fall ist das Ergebnis ![]() 0.000004431 und im 2. Fall nur
0.000004431 und im 2. Fall nur ![]() 0.000000084 vom exakten Ergebnis entfernt.
0.000000084 vom exakten Ergebnis entfernt.
Positionen können im Zeichnungsfenster der zwei- und dreidimensionalen Funktion über die Positionsabfrage einfach untersucht werden. Im Fenster der Funktion drücken Sie die Schaltfläche ![]() , oder drücken Sie im Zeichnungsfenster die linke Maustaste. Die Position wird im zweidimensionalen direkt übernommen. Geben Sie in dem folgenden Eingabedialog die Ableitung an, die Sie in diesem Punkt interessiert, und drücken Sie dann das Schaltfläche
, oder drücken Sie im Zeichnungsfenster die linke Maustaste. Die Position wird im zweidimensionalen direkt übernommen. Geben Sie in dem folgenden Eingabedialog die Ableitung an, die Sie in diesem Punkt interessiert, und drücken Sie dann das Schaltfläche ![]() . In dem Eingabedialog können Sie natürlich auch noch andere Punkte untersuchen oder die Position korrigieren, indem Sie dafür nur die gewünschte x- Position im zweidimensionalen, bzw. x- und y- Position im dreidimensionalen eingeben. Auf diese Weise können Sie z.B. Polstellen (d.h. Unendlichkeitsstellen) untersuchen, oder die Steigung (d.h. die 1. Ableitung) in einem Punkt abfragen.
. In dem Eingabedialog können Sie natürlich auch noch andere Punkte untersuchen oder die Position korrigieren, indem Sie dafür nur die gewünschte x- Position im zweidimensionalen, bzw. x- und y- Position im dreidimensionalen eingeben. Auf diese Weise können Sie z.B. Polstellen (d.h. Unendlichkeitsstellen) untersuchen, oder die Steigung (d.h. die 1. Ableitung) in einem Punkt abfragen.
